Nagyobb mennyiségű adat elemzésekor, főként ha ezen adatok forrása valamilyen manuális bevitel, elég gyakran előfordul, hogy azért torzul elemzésünk/diagramunk vagy kimutatásunk, mert a manuális bevitel során hiba történt, azaz mondjuk valaki eggyel több nullát írt a száma végére, vagy éppen ellenkezőleg, egy nullával felülírt egy korábban berögzített számot - igen, erre lehet azt mondani, hogy eliminálni kell ezeket a hibalehetőségeket, de előfordulhat olyan eset, amikor már csak hozott anyagból dolgozunk.

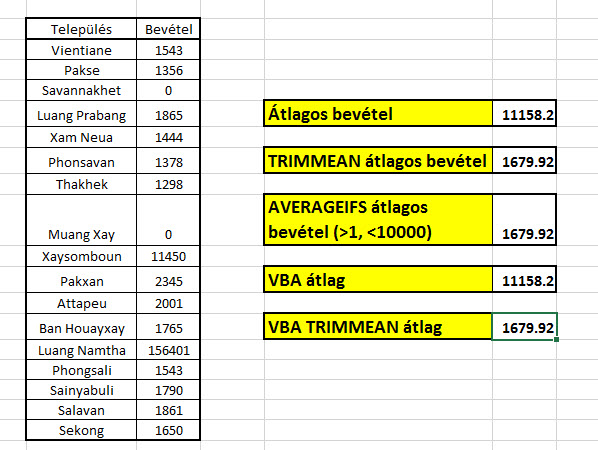
Mint például a következő kis mintatáblázat, amelynél tökéletesen látszik, hogy azért torzul az átlagunk, mert egyes cellákban nulla vagy éppen túlságosan nagy szám szerepel:

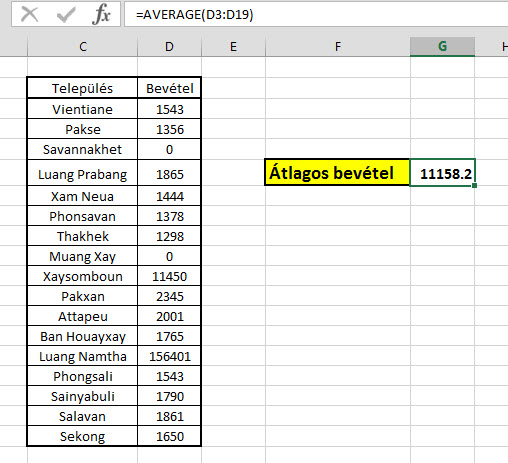De még nem is kell hibára gondolnunk, simán megtörténhet, hogy egyszerűen azokhoz a cellákhoz vagy nincs adatunk, vagy tényleg valamilyen különös okból kiugró eredményünk van - amit elemeznünk kell tovább, mindenesetre valóságosabb átlageredményt szeretnénk kimutatni.

Erre, ahogy az Excelben szinte mindenre, több megoldási lehetőségünk van, elsőként az annyira nem ismert TRIMMEAN függvény siethet segítségünkre, amely roppant egyszerű módon, az első paramétereként megadott tartományból a második paramétereként megadott százaléknyi adatpontot kiveszi az átlagszámításból.

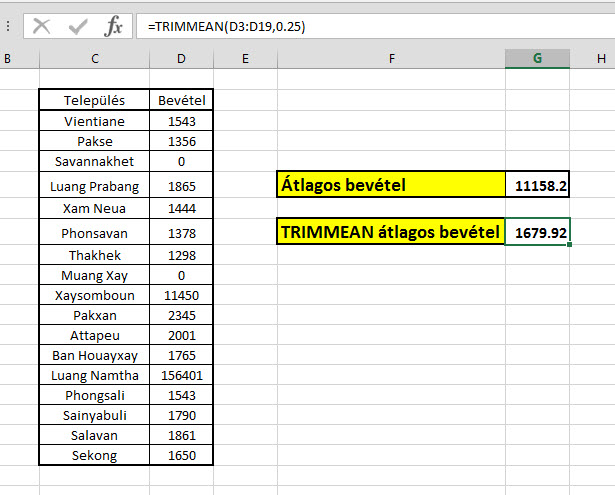
Tehát mostani példatáblánkat nézve:

=TRIMMEAN(D3:D19,0.25)

Ez azt jelenti, hogy a 17 városhoz tartozó értékünk lesz a tömb, majd mielőtt az átlagot kiszámolná, a függény eltávolítja az adatok 25%-át, értelemszerűen arányos módon, azaz a legalacsonyabb és legmagasabb értékekből ugyanannyit.

Jelen esetünkben ez azt jelenti, hogy 17 darab érték van a D3:D19 tartományban, ha 17-nek vesszük a 25%-át, akkor 4.25-öt kapunk, majd ha ezt elosztjuk kettővel és kerekítünk, akkor látjuk is, hogy 2 értéket fog eliminálni fentről és lentről is, így kapjuk meg a valósághoz jóval közelebb álló átlagértékünket.

Tehát van két igen fontos tudnivaló a TRIMMEAN-ről és ezen tudnivalók egyébként be is határolják alkalmazási lehetőségeit:

- mindig szimmetrikusan működik, azaz fentről és lentről is ugyanannyi értéket zár ki az átlagból
- mindig kerekít

De ami igazán megmutatja, hogy nagyjából semmi szükségünk a TRIMMEAN függvényre, az pont két másik formula, az AVERAGEIF és AVERAGEIFS, mert mindkettő meghatározott feltételek alapján képes átlagot számolni, az első értelemszerűen csak egy feltétel szerint, a második pedig akár több feltétel alapján is.

Ergó nincs szükségünk szimmetriára, egyszerűen határozzuk meg azon tartományt, amelyben helyes értékeink lehetnek és már meg is van az az átlag, amit igazán szerettük volna elérni.

Ahogy a képen látható is, AVERAGEIFS függvényt használva megadhatjuk, hogy egynél nagyobb, de tízezernél kisebb számainkból számoljunk átlagot:

=AVERAGEIFS(D3:D19,D3:D19,">1",D3:D19,"<10000")

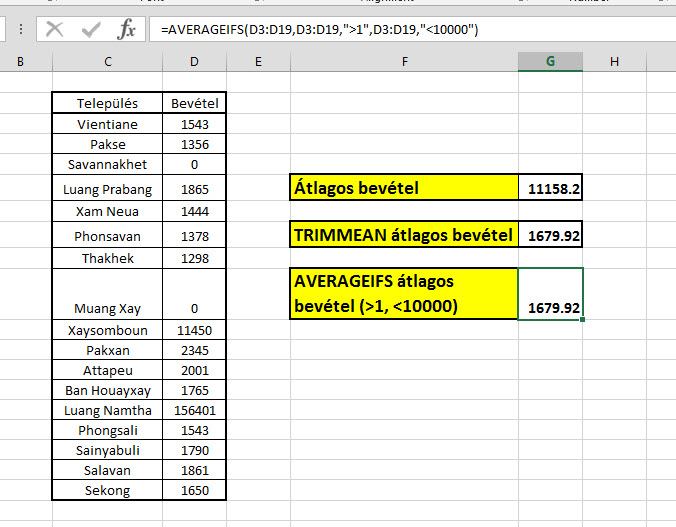Az első paraméter az a tartomány, ahol átlagolandó számaink szerepelnek, a második paraméter a kritérium tartománya, azaz itt akár már városaink nevére is írhatnánk feltételt, a harmadik kötelező paraméter pedig maga a kritérium - a többi pedig opcionális, feltételeink számától függően.

Persze azt ne felejtsük el, hogy VBA-ban is roppant egyszerűen végrehajtható műveletekről van szó, példának okáért az alábbi kód a G12 cellába fogja beírni a megadott tartományunk átlagértékét:

Persze, a tartomány és az eredmény is lehetne dinamikus, de most nem ez a lényeg. Ahogy látható is, a WorksheetFunction.Average metódus a lelke a történetnek, amely az ugyanilyen névre hallgató formula VBA leképezése.

És hát nem kell se programozónak, se tapasztalt VBA ismerőnek lenni ahhoz, hogy a fenti alapján lássuk a TRIMMEAN VBA-verzióját:

Azoknak persze, akik egész nap gyűrik a VBA-t és az Excelt, valószínűleg a fenti poszt minimális hozzáadott értékkel sem bír, de ha valakinek sikerült kicsit segíteni bármilyen feladatban vagy akár gondolatébresztőként volt segítség, már megérte.

És végül, ha van esetleg valakinek a fentiek után egy kicsit szórakozni az átlagolással, akkor álljon itt egy aprócska feladvány: hogy érjük el formulával (vagy akár VBA-val), hogy nagyság szerint csak minden második értékünk kerüljön be az átlagolandó populációba, majd abból számoljunk átlagot?